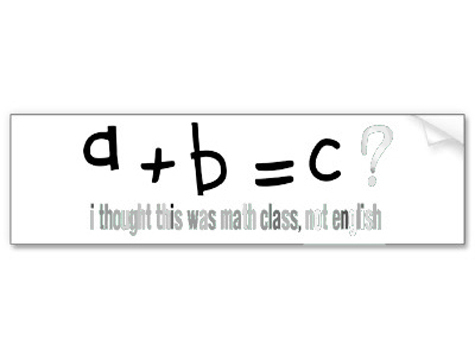Коллегам японского математика наверняка понадобится много времени, для того, чтобы разобраться в сложнейшем доказательстве. Тем не менее, если окажется, что АВС-гипотеза действительно доказана и получит статус теоремы, в руки математиков попадает мощнейший инструмент, каким теория чисел никогда не располагала. Чтобы дать читателю понять всю важность этой гипотезы, достаточно сказать, что с ее помощью Великая теорема Ферма, над которой почти четыре века безуспешно бились лучшие умы планеты, доказывается буквально в три строчки. И это лишь малая часть возможностей, заложенных в АВС-гипотезе. Ее называют самой интригующей гипотезой ХХ века и прочат ей статус самой знаменитой теоремы XXI века.
Еще одним достоинством гипотезы считается удивительная изящность и простота ее формулировки, свойственная математическим построениям средневековья. Конечно, слово "простота" здесь нельзя понимать буквально, но, действительно, любой человек, знакомый с арифметикой первого класса начальной школы, может разобраться в ней без излишнего труда.
Гипотеза имеет отношение к тройке взаимно простых (то есть не имеющих общих делителей) целых чисел а, в и с и устанавливает их взаимоотношение с математическим оператором под названием радикал (не путать с квадратным корнем). Она сравнительно молода, ее независимо друг от друга предложили в 1985 году математики Дэвид Мэссер и Джозеф Остерле, причем каждый из них наткнулся на нее случайно, занимаясь материями, далекими от теории чисел. До сих пор считалось, что если она и будет доказана, то явно нескоро. Однако сейчас есть основания полагать, что этот момент уже наступил, пишет cnews.ru.
Итак, формулируется abc-гипотеза в полном соответствии с названием, для троек натуральных чисел a, b и c. Предполагается, что эти числа не имеют общих делителей, превышающих единицу, и удовлетворяют условиям a < b и a + b = c. Чтобы продвинуться дальше, необходимо ввести понятие радикала числа n — rad(n), сообщает www.computerra.ru. Согласно основной теореме арифметики, любое натуральное n можно единственным образом (с точностью до порядка следования сомножителей) представить как произведение простых чисел, то есть в виде p1d1 • p2d2 •…• pkdk, где p1 < p2 <…< pk — простые, а d1, d2, …, dk — натуральные. Радикал же отличается от самогó n тем, что все степени dk приравниваются к единице; другими словами, rad(n) будет равен p1•p2•…•pk. Если мы возьмём, к примеру, числа 6, 24 и 36, то у каждого из них радикал равняется шести, а rad(20) = rad(80) = 10.
Обычно в упомянутых выше тройках радикал произведения a•b•c оказывается больше числа c. Найти несколько исключений из правила несложно: имеются довольно очевидные наборы (1, 8, 9), (5, 27, 32) и (32, 49, 81), а компьютер, если ограничиться c < 50 000, обнаружит ещё 273 примера. Легко доказать и то, что «исключительных» троек, имеющих rad(a•b•c) < c, бесконечно много (существует, скажем, их серия a = 1, b = 9n – 1, c = 9n).
Именно «исключительные» тройки и интересовали авторов abc-гипотезы. Согласно ей, для любого ε > 0 существует лишь конечное число наборов (a, b, c), которые удовлетворяют условию c > rad(a•b•c)1 + ε. Иначе говоря, при ε = 0 количество наборов, как мы установили выше, бесконечно, но ситуация должна меняться даже при ε = 0,001 или 0,0001.
Силу этого утверждения прекрасно характеризуют его следствия, к которым относится, в частности, Великая теорема Ферма, объявляющая, что уравнение xn + yn = zn не имеет натуральных решений для любого целого n > 2. Связь между теоремой и гипотезой станет очевидной, если рассмотреть другую формулировку последней: для любого ε > 0 и всевозможных троек (a, b, c) должна существовать такая константа К, что c всегда будет уступать выражению К•rad(a•b•c)1 + ε. В этой формулировке каждому значению ε соответствует своя константа, и мы можем взять (пока — гипотетически) верный случай ε = 1 и К < 1, который ведёт к неравенству c < rad(a•b•c)2.
Далее мы заменяем xn, yn и zn на a, b и c, после чего записываем серию бесспорных соотношений rad(a•b•c) = rad(xn•yn•zn) = rad(x•y•z) ≤ x•y•z < z3. Поскольку c заменяет zn и уступает rad(a•b•c)2, можно записать, что zn < (z3)2 = z6. При n ≥ 6 это неравенство, разумеется, выполняться не будет, что свидетельствует в пользу теоремы Ферма.
Из истинности гипотезы Эстерле и Массера следует и «более общее», чем Великая теорема, утверждение, известное как гипотеза Ферма — Каталана. Она говорит о том, что уравнение ad + be = cf имеет только конечное число решений (a, b, c, d, e, f), где a, b, c — натуральные взаимно простые числа, а d, e, f — натуральные, удовлетворяющие неравенству d–1 + e–1 + f–1 < 1. Строго говоря, если a или b, как в упомянутом выше случае 1 + 8 = 9, приравнять к единице, решений будет бесконечно много (единицу можно возводить в сколь угодно большую степень), но при формулировке гипотезы Ферма — Каталана они принимаются за одно.
«Чтобы осмыслить выкладки Мотидзуки, придётся потратить огромное количество времени, — говорит представитель Стэнфордского университета Брайан Конрад. — Но сделать это необходимо, поскольку найденные им оригинальные методы и подходы могут упростить решение других задач из теории чисел».
Самое общее представление об идеях Синити Мотидзуки даёт дискуссия на сайте MathOverflow, но даже здесь нужна очень серьёзная математическая подготовка.